Seus postulados são os seguintes:

1) um gás perfeito é um sistema formado por um grande número de partículas consideradas como esferas rígidas de diâmetro d, dotadas de movimento caótico;

2) suas partículas tem massa mi > 0, mas o tamanho das moléculas (volume) é pequeno ( desprezível) em comparação com a distância média entre elas e o tamanho do frasco que contém o gás;

3) as partículas não exercem forças de interação (atração ou repulsão) apreciáveis entre si, exceto nas colisões que são elásticas;

4) toda energia interna se encontra na forma de energia cinética translacional;

5) possuem velocidade e obedecem as leis de Newton;

6) propagam-se em linha reta;

7) os choques com as paredes do recipiente são perfeitamente elásticos, isto é, a energia cinética não pode ser convertida em outras formas, como por exemplo o calor.

A partir destes postulados, podemos tirar as seguintes conclusões:

1) ao se estabelecer que o tamanho molecular é pequeno, queremos firmar a idéia de que o somatório dos volumes de todas as partículas é desprezível, isto é, existem poucas partículas, em outra palavras, estamos assumindo que o sistema se encontra em baixa pressão;

2) afirmar que as partículas não exercem forças de interação apreciáveis, também implica na existência de um número pequeno de partículas; conseqüentemente, também estamos assumindo que o sistema se encontra em baixas pressões;

3) para terem energia cinética translacional, as partículas constituintes do gás só podem estar associadas a átomos ou partículas monoatômicas, uma vez que moléculas poliatômicas possuem energias cinéticas de vibração e de rotação. Com estes postulados, temos duas alternativas para desenvolver a Teoria Cinética dos Gases:

a) sem levar em conta o tamanho das partículas, mas aceitando os vínculos vi 0 e fi 0, o modelo reproduz a equação de Clapeyron; contudo, com essas condições somente são válidas em situações de pressões muito baixas (P 0), elas limitam a aplicação do modelo às regiões onde elas possam ser verificadas. Este modelo é comumente denominado "modelo de gás ideal";

b) levando em conta o tamanho das partículas, existirá um volume de moléculas que deve ser descontado do volume total do recipiente, a fim de se obter espaço livre para o gás; considerando ainda a ausência das forças intermoleculares, o modelo irá reproduzir a seguinte equação, conhecida como equação de Hirn:

e não a equação de Clapeyron.

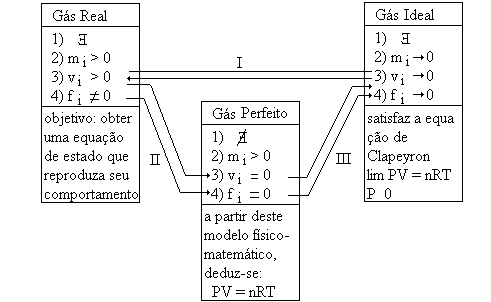
          Comparando as considerações apresentadas anteriormente para os gases reais e perfeito, deparamo-nos com o seguinte problema: temos um gás real cujas propriedades P, V e T, podem ser determinadas experimentalmente e para o qual queremos obter uma equação chamada de "Equação de Estado", que apresente boa concordância quando comparada com valores experimentais. Em contrapartida, temos uma equação teórica, válida para um gás que não existe! Além disso, temos equações empíricas, obtidas de resultados experimentais sobre o comportamento dos gases reais, em condições particulares, que concordam com as conclusões da Teoria Cinética dos Gases Perfeitos. O gás ideal desempenha o elo entre o gás real e o gás perfeito, com o objetivo de dar coerência à situação apresentada anteriormente. Nestas condições, o gás ideal é um gás real, submetido a determinadas condições, em geral P 0, tais que sejam satisfeitos os seguintes vínculos:

1) o volume vi das partículas é muito pequeno em relação ao volume V do recipiente. Nestas condições temos:

2) as distâncias entre as partículas são tão grandes que as forças de interação entre elas são muito fracas; isto quer dizer que podemos escrever:

fi 0

          Esses vínculos podem ser observados se adotarmos as seguintes condições:

P 0 ou T

          Como é muito mais fácil trabalhar com a condição P 0 (a outra, T , além da dificuldade de operação, fica limitada pela dissociação da partícula), esta é a condição mais empregada para se obter a equação do "gás ideal". Com essas considerações, a equação que representa, rigorosamente, o comportamento de gás ideal é:

lim P.V = n.R.T

p0

          Portanto, um gás ideal é um gás para o qual temos: massa mi > 0, volume vi 0 e forças de interação fi 0.

          Com essas definições de gás real, perfeito e ideal, e suas interações, é mais fácil compreender e entender a evolução do estudo do gases. No esquema que segue, apresentamos as características mais marcantes de cada definição e do elo entre elas.

I) modelo teórico;

II) modelo do gás ideal, a partir das condições do gás perfeito;

III) levantando as duas condições limites do gás ideal, deve-se obter a equação para gás real.

          A partir das definições propostas anteriormente, podemos tirar as seguintes conclusões:

1) Levine, I.N., Physical Chemistry, McGraw-Hill Kogakusha, I. S. ed, Tokyo, 1978.

2) Moore, W. J., Físico-Química, vol. 1 trad. 4a ed, Editora Edgard Blucher Ltda, 1976.

3) Atkins, P. W., Physical Chemistry, Oxford University Press, Oxford, Fifth ed. 1944

4) Fried, V., Hameka, H. F., Blukis, U., Physical Chemistry, Mcmillan Publishing Co., Inc.; N. Y.. 1975.

5) Bauman, R. P., Moren Thermodynamics with Statistical Mechanics. Macmillan Publishing Co., N. Y., 1972.

6) Brescia, F. Arents, J. Meislich, H. & Truk General Chemistry, John Wiley & Sons, N. Y., 1976.

7) Eggers Jr, N. W., Halsey Jr, G. D. & Rabinovitch, B. S., Físico-Química, Editorial Limusa-Wiley S. A ., México, 1967.

8) Berry, R. S., Rice, S. A . Ross, J., Physical Chemistry, John Wiley & Sons, N. Y., 1976.

9) Pitzer, K. S., Brewer, L., Thermodinamics, second ed., McGraw-Hill Book CoTokyo, 1961.

10) Daubert, T.E., Chemical Engineering Thermodynamics McGraw-Hill Book Co., Int. Ed., Singapore, 1985.

11) Abott, M.M. e Van Ness, H. C., Termodinâmica, McGraw-Hill, Portugal 1992.

12) Glasstonne, S., Tratado de Química Física, Aguilar Ed., Madrid, 1976

13) Sears, F., Zemansky, M. W. & Young, H. D., Física, v. 2, 2a Ed., Livros Técnicos e Científicos Editora, R.J., 1984.

14) McKelvey, J,P. & Groth, H., Física, vol.2, Harper & Row do Brasil, S.P., 1978.

15) Tripler, P. A., Física para Cientistas e Engenheiros, vol.2, terceira ed., Ed. Guanabara Koogan S. A ., R. J., 1994.

16) Kauzmann, W., Teoria Cinética de los Gases, Editorial Reverté, S. A ., Barcelona, 1970.

17) Pilla, I., Físico-Química, vol. 1, Livros Técnicos e Científicos S. A ., 1979.

18) Alberty, R. A., Sibey, R. J., Physical Chemistry, John Wiley & Sons Inc., Singapore, 1992.

19) Maron, S. H. & Prutton, C. F., Fundamentos de Físico Química, Editorial Limusa, México, 1980.

20) Mahan, B. & Myers, R. J., Química - Um Curso Universitário, trad. 4a. ed., Editora Edgard Blucher Ltda, S.P., 1995.

21) Brady, J. e . & Humiston, G. E., Química Geral, vol. 1, 2a ed., Livros Técnicos e Científicos Editora S. A ., 1986.

22) Russell, J. B. Química Geral, vol. 1, 2a ed. Makron Books Editora Ltda, S.P., 1994.

23) Catellan, G., Fundamentos de Físico-Química, Livros Técnicos e Científicos Editora, R. J., 1995.

24) Lask, A . M., J. Chem. Educ., 51, 141 (1974).

25) Cagle Jr, F. W., Chem. Educ.,692 (1973).

26) Deal, W. J., Chem. Educ., 405-407 (1975).

27) Herron, J. D., Chem. Educ., 530-531.

28) Levine, S., Chem. Educ.,399 (1985).

29) Pilar, F. L., Chem. Educ.,284-285 (1967).