Home | Revistas | Nossos Livros | Links Amigos
Isidoro de Sevilha(publicado originalmente em Signum, Revista da ABREM -
Associação Brasileira de Estudos Medievais, São Paulo, No. 4, 2002.
Reproduzido aqui, por especial cortesia da ABREM)Estudo Introdutório - a Aritmética de Isidoro de Sevilha
e a Educação Medievaltradução do original / original Latino
Jean Lauand
Prof. Titular da Faculdade de Educação da
Universidade de São Paulo
Isidoro e o livro das Etimologias
Apresentamos ao leitor uma edição bilíngüe (original latino [1] / tradução ao português) da Aritmética - capítulos 1 a 7 do Livro III: De Mathematica, do Etymologiarum libri XX de Isidoro de Sevilha.
Santo Isidoro (c. 560-636), nascido em Sevilha na época visigoda, foi bispo nesta cidade de 600 a 636. Ele representa um dos grandes elos de transmissão da cultura clássica para a Idade Média. Sua obra Etimologias é uma espécie de enciclopédia, muitíssimo utilizada como tal ao longo de toda a Idade Média: mesmo em autores muito posteriores, como Tomás de Aquino, encontram-se inúmeras referências a esta obra. Ao examinar uma questão qualquer, o autor medieval costumava analisar a etimologia das palavras envolvidas na discussão. Não o fazia para ostentar erudição, mas por basear-se na convicção de que a origem da palavra podia conter em si informações sobre a própria realidade referida.
Etimologias é mais do que um livro sobre a linguagem: expressa todo um panorama da época e sua visão-de-mundo. Compõe-se de vinte livros, cada um elucidando palavras de um determinado campo do saber: I. Gramática; II. Retórica e Dialética; III. Matemática (Aritmética, Geometria, Música e Astronomia); IV. Medicina; V. As leis e os tempos; VI. Os livros e os ofícios eclesiásticos; VII. Deus, os anjos e os santos; VIII. A Igreja e outras religiões; IX. Línguas, povos, reinos, milícia, cidades e parentesco; X. Etimologia de palavras diversas; XI. O homem e os seres prodigiosos; XII. Os animais; XIII. O mundo e suas partes (elementos, mares, ventos etc.); XIV. A terra e suas partes (Geografia); XV. As cidades, os edifícios e o campo; XVI. As pedras e os metais; XVII. A agricultura; XVIII. Guerra, espetáculos e jogos; XIX. Naves, edifícios e vestimentas; XX. Comida, bebida e utensílios.
Nesses vinte livros (e internamente em cada livro) aparece uma original e surpreendente organização dos dados para consulta e esta é a razão pela qual Isidoro é - neste momento em que escrevemos, outubro de 2001 - com toda a justiça, o "candidato" mais indicado para Padroeiro da Informática e da Internet [2] .
O gosto que os autores medievais tinham pela etimologia [3] derivava de uma atitude com relação à linguagem bastante diferente da que, geralmente, temos nós hoje. Na Idade Média, ansiava-se por saborear a transparência de cada palavra; para nós, pelo contrário, a linguagem é opaca e costuma ser considerada como mera convenção (e nem reparamos, por exemplo, em que: "coleira", "colar", "colarinho", "torcicolo" e "tiracolo" se relacionam com "colo", pescoço). Naturalmente, ao tratar da aritmética as análises etimológicas (sugestivas, embora tantas vezes falsas ou forçadas em Isidoro e nos autores medievais) não são tão importantes; mais decisivo é o conhecimento dessa disciplina, que terá na enciclopédia de Isidoro um dos principais referenciais de ensino para a Idade Média.
Referencial pobre (nem poderia ser diferente naqueles atribulados tempos), sobretudo no que se refere ao livro III, dedicado ao quadrivium, às quatro artes matemáticas: Aritmética, Geometria, Música e Astronomia. Em todo caso, mais do que aspectos "técnicos" da aritmética das Etimologias, interessa-nos aqui o uso pedagógico que o legado isidoriano propiciará à Idade Média. Isidoro não apresenta (nem pretende fazê-lo) inovações científicas; tudo o que quer é iluminar, na medida do possível, a época de trevas em que está instalado. Nessa "cultura de resumos" que é a transição do mundo antigo para o medieval, Isidoro apresenta os elementos que considera essenciais para sua "enciclopédia". Neste estudo introdutório, destacaremos alguns aspectos - referentes à Aritmética - desse trabalho de ponte entre a cultura da Antigüidade e a da Idade Média, feita pela enciclopédia Etymologiarum.
Isidoro começa designando as matemáticas "doctrinalis scientia", ciência do conhecimento [4] , que trata da "quantidade abstrata" [5] .
Aos fundadores da Matemática, está dedicado o capítulo 2 [6] .
No capítulo 3, apresenta a tradicional concepção de número como "multitude" (multitudo [7] ) e, assim, o um não é número, mas a origem do número, concepção euclidiana e aristotélica (p. ex. Metaph. 1088 a 6). Nesta mesma linha, Tomás de Aquino, em seu tratado De Deo Uno, assim discute a unidade: "O um, que é princípio dos números, opõe-se à multitude, que é o número, como medida em relação ao medido. Pois o um tem o caráter de primeira medida, e o número é multitude medida pelo um, como fica claro pela Metafísica de Aristóteles". (Summa Theologica I, 11, 2).
Nos tópicos seguintes deste estudo destacaremos alguns aspectos pedagógicos (referentes ao cap. 4 de Isidoro) e matemáticos (dos cap. 4, 5 e 7). No capítulo 6, após estabelecer a divisão entre a consideração do número em si mesmo e em relação a outro, Isidoro - para tratar, de algum modo, de "frações" - define os números: superparticulares, superpartientes, múltiplos superparticulares, múltiplos superpartientes, subsuperparticulares, subsuperpartientes etc., que são muito utilizados no tratado de música de Boécio.

Ilustração da edição de Friedlein do De Musica de Boécio
Números superficiais
Diversos conceitos apresentados na Aritmética de Isidoro são recolhidos dos gregos (valendo-se de autores como Boécio [8] e Cassiodoro), como é o caso de:
Números triangulares (no arranjo tradicional pitagórico), como o 3, 6, 9 e 16:..

Números quadrados, como o 4, 9, 16, 25...

Números pentagonais, como o 5, 12, 22...

Etc.
Menciona também os números piramidais.
O primeiro número piramidal (de tetrágono) é 1. O segundo número piramidal é 5, soma do vértice, 1, ao plano do número quadrado, 4. O terceiro é 14: 1 +5 +9. O quarto é 30. Etc.
o vértice
------
o o
o o plano de 22

o o o
o o o plano de 32
o o o
-----
o o o o
o o o o plano de 42
o o o o
o o o o
Certamente, o uso desses conceitos na primeira Idade Média será muito restrito: faltam as articulações teórico-demonstrativas dos gregos estão ausentes: durante séculos os teoremas estarão praticamente ausentes. No caso dos números associados a figuras faltam em Isidoro até mesmo os resultados mais interessantes e fáceis, como o de que a soma dos n primeiros números ímpares é o número quadrado de lado n (a que é dedicado o capítulo II, 12 da Aritmética de Boécio):

1 + 3 + 5 + (2n-1) = n2
A aritmética como base da alegoria na pedagogia de Isidoro
A importância da aritmética para a educação é indicada pelo próprio Isidoro no capítulo 4: "A importância dos números" (III, 4). Como não podia deixar de ser, a aritmética serve também aos estudos de religião, o grande "tema transversal" na pedagogia medieval.
Na leitura profundamente alegórica que a Idade Média faz da Bíblia, a interpretação do "significado" dos números é de capital importância. O próprio Isidoro explicita: "Em muitas passagens da Sagrada Escritura se mostra quão profundo é o mistério que (os números) encerram. Não em vão, em louvor de Deus, diz a Escritura: 'Tudo fizeste com medida, número e peso' (Sab 11, 21)".
Esse princípio é - desde o fim da Antigüidade e ao longo da Idade Média - levado muito a sério. Se para um cristão de hoje os números na Bíblia têm, quando muito, uma importância genérica, a interpretação da Bíblia, na época, requer um conhecimento da Aritmética e do significado místico dos números.
Por exemplo, é necessário saber o que significa o número 153, quando o Evangelho diz que os apóstolos, na pesca milagrosa após a ressurreição de Cristo, apanharam 153 peixes. E vemos um S. Agostinho, repetidas vezes em seus sermões explicar esse 153, pois considera o simbolismo numérico um elemento importante para a compreensão da Revelação:
"Estes 153 são 17. 10 por quê? 7 por quê? 10 por causa da lei, 7 por causa do Espírito. A forma septenária é por causa da perfeição que se celebra nos dons do Espírito Santo. Descansará -diz o santo profeta Isaías- sobre ele, o Espírito Santo (Is 11,23) ... (com seus 7 dons) ...
Já a lei tem 10 mandamentos (...) Se ao 10 ajuntarmos o 7 temos 17. E este é o número em que está toda a multidão dos bem-aventurados. Como se chega, porém, aos 153? Como já vos expliquei outras vezes, já muitos me tomam a dianteira. Mas não posso deixar de vos expor cada ano este ponto. Muitos já o esqueceram, alguns nunca o ouviram. Os que já o ouviram e não o esqueceram tenham paciência para que os outros ou reavivem a memória ou recebam o ensino. Quando dois são companheiros no mesmo caminho, e um anda mais depressa e o outro mais devagar, está no poder do mais rápido não deixar o companheiro para trás. (...) Conta 17, começando por 1 até 17, de modo que faças a soma de todos os números, e chegarás ao 153. Por que estais à espera que o faça eu? Fazei vós a conta" [9]
Assim, não é de estranhar que num Rábano Mauro, discípulo de Alcuíno, encontremos todo um Tratado sobre o significado místico dos números [10] , discutindo, caso a caso, o significado dos números na Bíblia. O cristão de hoje sorri ao ler o autor medieval, munido de calçadeira, explicar que o número 120 é soma da progressão aritmética: 1+2+3...+14+15, e que isto representa misticamente aquelas passagens de Atos em que se descreve a vinda do Espírito Santo (At 2, 1) quando estava reunida a assembléia de 120 pessoas (At 1,15) "todos num mesmo lugar" (a soma simboliza essa reunião).
Precisamente nessas diferenças é que se capta a mentalidade da época. O homem medieval está seriamente convencido de que não há palavra ociosa na Sagrada Escritura e que tudo o que está revelado "é inspirado por Deus, e útil para ensinar, para repreender, para corrigir e para formar na justiça" (II Tim 3, 16)."
Se a dimensão religiosa é essencial para a pedagogia de Isidoro, ele não descura os aspectos práticos (entre os quais se incluem a organização da vida pelas horas, introduzida por São Bento): " Em alguma medida, nossa vida dá-se sob a ciência dos números: por ela sabemos as horas, acompanhamos o curso dos meses, sabemos quando retorna cada época do ano. Pelo número aprendemos a evitar enganos. Suprimido o número de todas as coisas, tudo perece. Se se tira o cômputo dos tempos, tudo ficará envolto na cega ignorância e o homem não se pode diferenciar dos animais, que ignoram os procedimentos de cálculo".
Um conceito: número perfeito
Na linha da aplicação dos estudos de aritmética à leitura da Bíblia, analisemos mais de perto um conceito: o de número perfeito. Isidoro exemplifica com o número 6, que evidencia a perfeição (dos seis dias) da criação do mundo. Recolhendo o critério antigo, Isidoro define como perfeito o número cuja soma de seus divisores o perfaz. Assim, um número perfeito - é um número n, tal que a soma de seus divisores (a menos do próprio n) dá n. Se essa soma for maior do que n, o número diz-se abundante; se menor, deficiente.
Isidoro sabe que 6, 28, 496 e 8128 são perfeitos. E conhece o critério para a geração de números perfeitos:
p = (2n - 1). 2n-1 será perfeito, se (2n - 1) for primo.
Assim,
6 = (22 - 1). 2(2-1) é perfeito, pois (22 - 1) = 3 é primo.
28 = (23 - 1). 2(3-1) é perfeito, pois (23 - 1) = 7 é primo.
496 = (25 - 1). 2(5-1) é perfeito, pois (25 - 1) = 31 é primo.
8128 = (27 - 1). 2(7-1) é perfeito, pois (27 - 1) = 127 é primo.
Essa equação recebe uma formulação equivalente em Boécio. Boécio começa o capítulo sobre a geração dos números perfeitos (Aritmética I, 20) da maneira mais medieval possível: observando a grande semelhança entre os números perfeitos (raros e bem ordenados) e as virtudes, e a dos números imperfeitos e os vícios, etc. A seguir, explica como se dá a "geração e procriação" dos números perfeitos: a partir da seqüência dos números parmente pares (isto é, as potências de 2):
1, 2, 4, 8, 16, 32, 64, 128 ...
Somam-se os n primeiros. Se essa soma der um número primo, multiplica-se pelo maior somando, 2n-1, e obtém-se um número perfeito.
De fato, os 2 processos são equivalentes, pois:
1 + 2 + 4 + + 2n = 2n - 1.
E, assim, a fórmula boeciana fica: (2n - 1) . 2n-1, que é a fórmula que tínhamos enunciado originalmente.
Esses conceitos matemáticos, que Isidoro repassa - em formulação sumária - para a Idade Média, reaparecem, por exemplo, em torno do ano 1000, em outro importante momento pedagógico medieval: a peça Sabedoria, que marca a re-invenção - por Rosvita de Gandersheim [11] - da composição teatral no Ocidente.
Na peça, a autora, com claros propósitos didáticos, brinda-nos com uma aula de Matemática (em III, 31 e ss). Trata-se da cena em que Adriano, o imperador pagão, em meio ao interrogatório para demover de sua fé a nobre senhora cristã Sabedoria - e suas três filhinhas Fé, Esperança e Caridade (sempre, a alegoria) -, pergunta a idade das meninas. Sabedoria aproveita "a deixa" para desenvolver conceitos aritméticos expostos por Isidoro, como:
número parmente par - são as nossas potências de 2.
parmente ímpar - o dobro de um número ímpar.
imparmente par - produto de um ímpar por um parmente par.
número perfeito, número abundante, número deficiente. Etc.
SABEDORIA: Ó Imperador, se tu perguntas a idade das meninas: Caridade tem por idade um número deficiente que é parmente par; Esperança, também um número deficiente, mas parmente ímpar; e Fé, um número abundante mas imparmente par.
ADRIANO: Tal resposta me deixou na mesma: não sei que números são!
SAB.: Não me admira, pois, tal como respondi, podem ser diversos números e não há uma única resposta.
ADR.: Explica de modo mais claro, senão não entendo.
SAB.: Caridade já completou 2 olimpíadas; Esperança; 2 lustros; Fé, 3 olimpíadas.
ADR.: E por que o número 8, que é 2 olimpíadas, e o 10, que é 2 lustros, são números deficientes? E por que o 12, que perfaz 3 olimpíadas, se diz número abundante?
SAB.: Porque todo número, cuja soma de suas partes (isto é, seus divisores) dá menor do que esse número, chama-se deficiente, como é o caso de 8. Pois os divisores de 8 são: sua metade - 4, sua quarta parte - 2 e sua oitava parte - 1, que, somados, dão 7. Assim também o 10, cuja metade é 5, sua quinta parte é 2 e sua décima parte, 1. A soma das partes do 10 é portanto, 8, que é menor do que 10. Já, no caso contrário, o número diz-se abundante, como é o caso do 12. Pois sua metade é 6, sua terça parte, 4, sua quarta parte, 3, sua sexta parte, 2 e sua duodécima parte, 1. Somadas as partes, temos 16. Quando, porém, o número não é excedido nem inferado pela soma de suas diversas partes, então esse número é chamado número perfeito. É o caso do 6, cujas partes - 3, 2, e 1 - somadas, dão o próprio 6. Do mesmo modo, o 28, 496 e 8128 também são chamados números perfeitos.
ADR.: E quanto aos outros números?
SAB.: São todos abundantes ou deficientes.
ADR.: E o que é um número parmente par?
SAB.: É o que se pode dividir em duas partes iguais e essas partes em duas iguais, e assim por diante, até que não se possa mais dividir por 2, porque se atingiu o 1 indivisível. Por exemplo, 8 e 16 e todos que se obtenham a partir da multiplicação por 2, são parmente pares.
ADR.: E o que é parmente ímpar?
SAB.: É o que se pode dividir em partes iguais, mas essas partes já não admitem divisão (por 2). É o caso do 10 e de todos os que se obtêm, multiplicando um número ímpar por 2. Difere, pois, do tipo de número anterior, porque naquele caso, o termo menor da divisão é também divisível; neste, só o termo maior é apto para a divisão.
(...)
ADR.: E o que é imparmente par?
SAB.: É o que - tal como o parmente par - pode ser dividido não só uma vez, mas duas e, por vezes, até mais. No entanto, atinge a indivisibilidade (por 2) sem chegar ao 1.
ADR.: Oh! que minuciosa e complicada questão surgiu a partir da idade destas menininhas!
SAB.: Nisto deve-se louvar a supereminente sabedoria do Criador e a Ciência admirável do Artífice do mundo: pois, não só no princípio criou o mundo do nada, dispondo tudo com número, peso e medida, como também nos deu a capacidade de poder dispor de admirável conhecimento das artes liberais, até mesmo sobre o suceder do tempo e das idades dos homens.
Até um autor como Tomás de Aquino ainda discute "números perfeitos" e diversos critérios de perfeição numérica para a interpretação da Bíblia (pelos quais o 7, o 12 ou o 100 podem ser perfeitos). Note-se a elasticidade desses critérios em diversas passagens.
a) No Comentário às Sentenças, (d 15, q 3, a 1), Tomás lança a objeção de que Deus não pode ter consumado sua obra no sétimo dia, porque o número perfeito é 6. E responde considerando que o 6 é perfeito por causa de "suas partes", que somadas o perfazem. E trata-se de uma perfeição especial pois, no caso do 6, as partes - 1, 2 e 3 - sucedem-se de modo ordenado e contínuo (ordinatim et continue) e é essa perfeição que condiz com a dos 6 primeiros dias da criação.
b) Já em Comentário às Sentenças, (d 47, q 1, a 2), discutindo o número dos apóstolos, 12, diz: "o sete é o número da perfeição". Ora o 7 se compõe de 3 mais 4 e se multiplicarmos o 3 pelo 14, obteremos o 12, que é duas vezes o 6, que é número perfeito. Além do mais, na Catena Aurea in Matthaeum (cp 10 lc 1), a perfeição do 12 é atribuída à do 6 multiplicado por 2 (que representa os dois preceitos da caridade...).
c) Na Summa (II-II, 87, 1), o 10 aparece "de certo modo" (quodammodo) como número perfeito, pois é uma espécie de primeiro limite dos números, a partir do qual, ele retomam a ordem do um, dois etc.
d) Na Catena Aurea in Matthaeum (cp 8 lc 2), comentando a passagem do Evangelho do centurião, considera o 100 um número perfeito.
Como se vê, a importância de Isidoro projeta-se pelos séculos medievais e é abrangente e profunda.
ISIDORO DE SEVILHA – AS ETIMOLOGIAS
Livro III - Sobre a Matemática
Prefácio
Em latim, chama-se ciência do conhecimento à ciência ["matemática"] que trata da quantidade abstrata. A quantidade é abstrata quando no intelecto a separamos da matéria ou de outros acidentes, como é o caso de "par" e "ímpar", que só são considerados pelo raciocínio.
Há quatro dessas disciplinas: aritmética, música, geometria e astronomia.
A aritmética é a disciplina da quantidade numerável em si mesma considerada.
A música é a disciplina que trata dos números que se encontram nos sons.
A geometria é a disciplina que trata da magnitude [12] e das formas.
A astronomia é a disciplina que trata do movimento [13] dos astros do céu e contempla as características das estrelas.
A seguir, exporemos um pouco mais amplamente essas disciplinas para que possamos adequadamente mostrar seus princípios.
1. Sobre a denominação da disciplina aritmética
1. A aritmética é a disciplina dos números e os gregos chamam o número arithmón. Alguns autores profanos pretendem que ela seja a primeira entre as disciplinas matemáticas, pois não depende de nenhuma outra.
2. Já a música, a geometria e a astronomia seguem-se à aritmética: só com seu auxílio podem surgir e subsistir [14] .
2. Sobre seus autores
Afirma-se que, entre os gregos, Pitágoras foi o primeiro a escrever [15] sobre a disciplina do número e que, depois, Nicômaco ampliou esse trabalho, que, entre os latinos, foi traduzido primeiro por Apuleio [16] e depois por Boécio.
3. O que é o número
1. Número é uma multitude [17] constituída a partir de unidades, pois o um não é número, mas a origem do número. A palavra "número" procede de nummus (dinheiro), por seu uso freqüente. Um derivou seu nome do grego, pois o grego chama o um héna, tal como o dois e o três que eles chamam duo e tría.
2. O quatro tomou esse nome da figura quadrada. Já o cinco recebeu seu nome não segundo a natureza, mas pelo arbítrio da vontade de quem impôs nome aos números. O seis e o sete também procedem do grego.
3. Em muitas palavras que em grego começam por aspiração, nós a substituímos por um S. Assim, em vez de hex dizemos sex (seis) e septem (sete) em lugar de hepta, do mesmo modo que chamamos serpillum (serpilho) à erva herpillo. O oito foi trazido sem modificações; e o que é para eles ennéa, para nós é nove; e déka, dez.
4. Na etimologia grega, o dez é assim chamado porque ajunta e reúne os números que o antecedem: desmós significa em grego ajuntar ou reunir. Já viginti (vinte) é um dez duas vezes gerado (bis geniti), se trocarmos o B pelo V. Trinta (triginta) é um dez três vezes gerado e assim por diante, até o noventa.
5. O cem procede de cantho, círculo. Duzentos de dois centos e assim até mil. Mil deriva de multitude e daí também milícia, que é como "multitia"; e milhar, que os gregos, mudando uma letra, chamam de myriada.
4. A importância dos números
1. Não se deve desprezar a razão [18] que se encontra nos números. Em muitas passagens da Sagrada Escritura se mostra quão profundo é o mistério que encerram. Não em vão, em louvor de Deus, diz a Escritura: "Tudo fizeste com medida, número e peso" (Sab 11, 21).
2. Assim, o seis, que é um número perfeito - a soma de suas partes [19] o perfaz - evidencia a perfeição (dos seis dias) da criação do mundo. Assim também, sem o conhecimento dos números não se entende porque foram quarenta os dias em que Moisés, Elias e o próprio Senhor jejuaram.
3. E assim outros números aparecem também nas santas Escrituras cujo sentido figurado não se pode entender a não ser pelos que conhecem esta matéria. Em alguma medida, nossa vida dá-se sob a ciência dos números: por ela sabemos as horas, acompanhamos o curso dos meses, sabemos quando retorna cada época do ano.
4. Pelo número aprendemos a evitar enganos. Suprimido o número de todas as coisas, tudo perece. Se se tira o cômputo dos tempos, tudo ficará envolto na cega ignorância e o homem não se pode diferenciar dos animais, que ignoram os procedimentos de cálculo (rationem calculi).
5. Uma primeira divisão: números pares e ímpares
1. Os números se dividem em pares e ímpares. Os pares, por sua vez, se dividem em parmente pares, parmente impares e imparmente pares. Os números ímpares se dividem em: primos ou simples, segundos ou compostos e terceiros ou intermédios, que, de certo modo, são primos e não compostos e, de certo modo, são segundos e compostos.
2. Número par é o que se pode dividir em duas partes iguais, como o 2, o 4 e o 8. Já o ímpar não se deixa dividir em duas partes iguais, faltando ou sobrando 1 em uma delas. É o caso do 3, 5, 7, 9 etc.
3. Número parmente par é aquele que se pode dividir em partes iguais pares, sucessivamente, até atingir a indivisível unidade. Por exemplo, o 64, cuja metade é 32; a deste é 16; a deste é 8; a deste é 4; a deste é 2; a deste é 1, que é singular indivisível.
4. Número parmente ímpar é o que se deixa dividir em suas partes iguais, mas estas já não são divisíveis. É o caso do 6, do 10, do 38 e do 50. Assim que divides um desses números, obténs um número que não podes dividir.
5. Imparmente par é o número cujas partes podem ainda sofrer divisão, mas não a ponto de atingir a unidade. É o caso do 24, cuja metade é 12, que, por sua vez, tem por metade 6, cuja metade é 3, que não admite mais divisões e, assim, antes de atingir a unidade, chegamos a um termo que não se pode dividir.
6. Imparmente ímpar é um número que pode ser medido imparmente por número ímpar, como o 25 e o 49, ímpares que se dividem em partes ímpares: 49 é sete vezes sete e 25 é cinco vezes cinco.
Dos números ímpares, alguns são simples, outros compostos e outros médios.
7. São simples [20] os que não têm partes [21] exceto a unidade. Como o 3, o 5 e o 7. Estes só admitem uma parte [22] .
Os números compostos são os que não são medidos [23] só pela unidade, mas são obtidos também por outros números. É o caso do 9, do 15 e do 21, que são três vezes três, cinco vezes três e sete vezes três.
8. Números intermédios são os que, de certo modo, parecem primos e não compostos e, de outro modo, compostos. Como por exemplo o 9 em relação ao 25, é primo e não composto, pois não têm número [24] em comum, mas só a unidade (monadicum). Se comparamos, porém o 9 ao 15, ele é segundo e composto, porque têm número em comum além da unidade, o número 3 que mede o 9 em três vezes três e mede o 15 em três vezes cinco.
9. Dentre os números pares, por sua vez, há os que são abundantes, há os deficientes e há os perfeitos.
Os abundantes são os que, somando suas partes, excedem a sua própria plenitude. É o caso do 12, que tem cinco partes: a duodécima, que é 1; a sexta, 2; a quarta, 3; a terça, que é 4; e a metade, 6. Somando 1, 2 , 3, 4 e 6 obtém-se 16, que excede, em muito, o 12. E assim também muitos outros números como o 18 etc.
10. Números deficientes são aqueles que a soma de suas partes resulta menor do que esse número. Por exemplo, o dez, que tem três partes: a décima, 1; a quinta, 2; e a metade, 5. A soma de 1, 2 e 5 é 8 que, de longe, e menor do que 10. E o mesmo se dá com o 8 e com diversos outros números, cuja soma das partes é inferior ao próprio número.
11. Número perfeito é o que se perfaz com suas partes, como o 6. O 6 tem três partes: a sexta, 1; a terça, 2; e a metade, 3. Essas partes - 1, 2 e 3 - somadas consumam e perfazem o 6. São números perfeitos: na primeira dezena, o 6; na primeira centena, o 28; no primeiro milhar, o 496.
6. Sobre a segunda divisão dos números em geral
1. Todo número pode ser considerado em si mesmo ou em relação a outro. No primeiro caso, eles podem ser: iguais ou desiguais; no segundo, maiores ou menores. Os maiores se classificam em: múltiplos, superparticulares, superpartientes, múltiplos superparticulares, múltiplos superpartientes. Os menores se classificam em: submúltiplos, subsuperparticulares, subsuperpartientes, submúltiplos subsuperparticulares, submúltiplos subsuperpartientes.
2. O número considerado em si mesmo é considerado independentemente de relações com outro, como o 3, ou o 4, 5, 6 etc. O número considerado em relação a outro é examinado em comparação com outro. Como o 4 comparado ao 2 é dobro e múltiplo; e o mesmo se dá com o 6 em relação ao 3, o 8 em relação ao 4, o 10 em relação ao 5. Assim também o 3 é o triplo do 1; o 9 é triplo do 3 etc.
3. Dizem-se iguais os números que segundo a quantidade são iguais, como o 2 e o 2, o 3 e o 3, o 10 e o 10 e o 100 e o 100. São desiguais os números que, comparados, apontam para quantidades desiguais, como o 3 e o 2, o 5 e o 4, o 10 e o 6 e sempre um maior comparado a um menor ou um menor comparado a um maior dizem-se desiguais.
4. O número maior contém em si o menor ao qual é confrontado e algo mais; como por exemplo o 5 é mais que o 3, porque contém o três e outras duas partes mais. E assim também nos casos semelhantes.
5. O número menor está contido no maior ao qual é comparado, como o 3 em relação ao 5; que o contém e a duas partes. Múltiplo é um número que contém em si um menor duas, três, quatro ou mais vezes, como o 2 que é o dobro do 1, o três que é seu triplo, 4 seu quádruplo etc.
6. Já o contrário é o numero submúltiplo, que está contido duas, três, quatro ou mais vezes no múltiplo como, por exemplo, o 1 no 2 duas vezes; no 3, três; no 4, quatro; no 5, cinco; etc.
7. Superparticular é o número que contém em si o número inferior ao qual é comparado e além disso uma parte mais, como o 3 e o 2, que, quando comparados, o 3 contém o 2 e também o 1, que é meia parte do 2; o 4 e o 3, o 4 contém o 3 e o 1, que é a terça parte do 3; o 5 e o 4, o 5 contém o 4 e o 1 sua quarta parte; etc.
8. Número superpartiente é o que contém em si a todo número inferior e, além disso, duas, três, quatro, cinco ou mais partes dele, como, por exemplo, o 5 comparado ao 3, contém o 3 e duas partes dele; o 9 comparado ao 5 contém o 5 e quatro partes dele.
9. O número subsuperpartiente é o que se contém no superpartiente com algumas - duas, três ou mais - de suas partes, como, por exemplo, o 3 -com duas de suas partes- se contém no 5; e o 5 - com quatro de suas partes - se contem no 9.
10. O número subsuperparticular é o número menor que, junto com alguma de suas partes - meia, terça, quarta, quinta... - se contém no maior. Por exemplo, o 2 em relação ao 3; o 3 em relação ao 4; o 4 em relação ao 5; etc.
11. Múltiplo superparticular é o número que comparado com outro menor, contém em si múltiplas vezes esse número inferior e mais alguma parte dele, como por exemplo, o 5 em relação ao 2, contém o 2 duas vezes - isto é, 4 - e mais uma parte; o 9 comparado ao 4, contém duas vezes o 4 - isto é, 8 - e mais uma parte dele.
12. [Número submúltiplo [sub] subparticular é aquele que comparado a um maior, está contido nele múltiplas vezes e com uma parte sua. É o caso do 2 em relação ao 5: está duas vezes contido nele e mais uma parte sua]. O múltiplo superpartional é o número que, comparado com outro menor o contém múltiplas vezes e com outras partes dele. Por exemplo, o 8 em relação ao 3: o 8 contém o 3 duas vezes e mais duas partes dele. Eo 14 contém o 6 duas vezes e mais duas partes dele [ou o 16 contém o 7 duas vezes e mais duas partes dele e o 21 contém o 6 três vezes e mais três partes dele].
13. O número submúltiplo superpartional é aquele que comparado a um maior , está contido nele múltiplas vezes e com algumas partes suas. É o caso do 3 em relação ao 8: está duas vezes contido nele junto com duas parte suas. E o 4 está contido no 11 duas vezes junto com três partes suas.
7. Sobre a terceira divisão dos números em geral
1. Os números são discretos ou continentes. Neste caso, temos números lineares, superficiais e sólidos. Número discreto é o que está constituído por unidades discretas, como o 3, 4, 5, 6 etc.
2. Número continente é aquele que é constituído por unidades conexas, como por exemplo o 3 quando considerado em extensão, isto é, em linha, superfície ou corpo sólido. E o mesmo vale para o 4 ou o 5.
3. Número linear é aquele que começando com a unidade e seguindo uma linha vai até o infinito. Daí que seja designado por alfa, porque esta letra designa o 1 entre os gregos.
1--- 2 --- 3 --- 4 --- ...
4. O número superficial está contido não só por longitude mas também por latitude, como os números triangulares, quadrados, pentagonais ou circulares, assim como os que estão contidos no plano, isto é na superfície. E assim há números triangulares, quadrados e pentagonais (figuras abaixo).

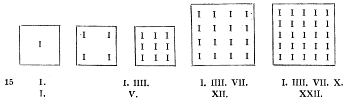
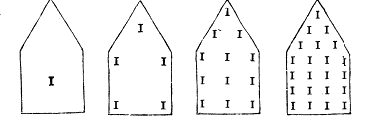
5. É circular [25] o número que multiplicado por si mesmo começa em si e volta a si, como 5 vezes 5, que é 25. Número sólido é o que está contido por longitude, latitude e altura, como ocorre com as pirâmides que se elevam a modo de chama.
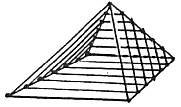
6. O cubo é como os dados.

A esfera possui uma redondez uniforme.

Número esférico é aquele que, multiplicado pelo circular, começa em si e volta a si. 5 vezes 5 é 25. Este círculo multiplicado por 5 de novo dá uma esfera, isto é 5 vezes 25 é 125.
[1] Seguimos o texto apresentado na edição de José OROZ RETA San Isidoro de Sevilla - Etimologías, Madrid, BAC, 1982.
[2] "Lo cierto es que el Papa Juan Pablo II evalúa nombrar a San Isidoro de Sevilla como santo patrono de los usuarios de Internet y los programadores de computación", informava o Portal Terra em janeiro de 2001 http://www.terra.com.ar/canales/tecnologia/11/11951.html . Cfr. também http://ar.clarin.com/diario/2001-02-09/s-04002.htm
[3] Examino com mais detalhe a importância da etimologia para Isidoro e para os autores medievais em J. LAUAND (org.) Cultura e Educação Medievais, São Paulo, Martins Fontes, 1999.
[4] Isidoro reserva a palavra latina doctrinalis para as quatro artes "matemáticas", as artes do quadrivium, tal como em grego mathema significa conhecimento. Assim, dirá ele: "Doctrinalis diuiditur in quattuor, id est, prima in Arithmeticam, secunda Musicam, tertia Geometricam, quarta Astronomiam" (2, 24, 10).
[5] Abstrato, para Isidoro, é o que foi separado, saído. Assim, por exemplo, falando dos dragões, Isidoro diz que eles freqüentemente provocam ciclones quando saem (abstractus) de suas cavernas: "Qui saepe ab speluncis abstractus fertur in aerem, concitaturque propter eum aer"(12, 4, 4).
[6] . .Sobre o cap. 2, recolho a seguinte nota do Dr. Sérgio Nobre "Isidoro escreve que Pitágoras foi o primeiro grego a escrever sobre a ciência dos números e que posteriormente fora completado por Nicomachus, cuja obra foi traduzida para o latim primeiramente por Apuleio e em seguida por Boécio. As informações históricas contidas neste verbete são importantes contribuições para aqueles que posteriormente viriam a escrever sobre a história das origens das teorias numéricas. Isidoro ressalta a figura do personagem de nome Pitágoras (c.580-500) ligado à Ciência dos Números. Embora Isidoro não mencione a existência de documentos que comprovam a existência de Pitágoras, pois certamente ele também se apóia em outros autores que o citam, este é mais um documento histórico que confirma a ligação deste com a matemática e especificamente com temas ligados a teoria de números. Outra informação histórica importante que aparece neste pequeno verbete é a existência de um outro grego que continuou os estudos iniciados por Pitágoras, ou por membros da Escola Pitagórica. Isidoro cita Nicômaco de Gerasa (~100 A.D.), pitagórico que, além de escritos matemáticos, também teve uma grande produção em textos sobre teoria musical. Sobre a obra matemática de Nicômaco, Isidoro não menciona o título, certamente deve ser o seu texto mais conhecido Introdução à aritmética, mas explicita que esta obteve duas traduções para o latim. Com relação às traduções para o latim, Isidoro menciona que a obra de Nicômaco foi primeiramente traduzida por Apuleio e em seguida por Boécio. São duas informações importantes para a compreensão do desenvolvimento histórico relativo às traduções de textos gregos para o latim. Primeiramente é citado Apuleio de Madaura (c.125-171), um sofista e platônico provavelmente do século II da Era Cristã, do qual muito pouco se sabe, e muito menos sobre suas atividades relacionadas à matemática. Cabe ressaltar que dentre as poucas informações que se tem atualmente sobre Apuleio, algumas são originárias das menções feitas a ele por Cassiodoro e Isidoro. Caso fosse encontrada, certamente esta tradução da obra de Nicômaco feita por Apuleio teria sua dose de contribuição para a compreensão do pensamento romano-europeu no início da era Cristã. Um segundo autor citado por Isidoro como tradutor da obra de Nicômaco foi o erudito Anicius Boethius". S. NOBRE, "Isidoro de Sevilha", in Elementos historiográficos da Matemática presentes em enciclopédias universais. Dissertação apresentada como requisito para a obtenção do título de Livre-Docente em História da Matemática. Unesp - campus de Rio Claro, 2001.
[7] Numerus autem est multitudo. Preferimos a forma nova multitude, pois multidão está demasiadamente associado a pessoas.
[8] Anicii Manlii Torquati Severini BOETII De Institutione Arithmetica libri duo. De Institutione Musica libri quinque. Edidit Godofredus Friedlein, Lipsiae, Teubner, 1867. Há ed. eletrônica em: http://cdl.library.cornell.edu/Hunter/hunter.pl?handle=cornell.library.math/cdl274&id=1
[9] . Sermão 250 in AGOSTINHO Sermões para a Páscoa, trad. de António Fazenda, Lisboa, Verbo, 1974.
[10] PL CXI, livro XVIII, cap. III do De Universo. Há tradução brasileira em J. LAUAND O significado místico dos números, Curitiba-S. Paulo, PUC-PR - GRD, 1992.
[11] . PL 137, 1035 - 1042. Há tradução brasileira em J. LAUAND Educação, Teatro e Matemática Medievais, São Paulo, Perspectiva, 2a. ed., 1990.
[12] Em 3, 10, Isidoro lembrará que geo-metria tem que ver com medida.
[13] Se a Astronomia trata do movimento, a Geometria é "disciplina magnitudinis inmobilis" (2, 24, 15).
[14] Do mesmo modo, comenta Boécio, que só se pode falar em homem se antes se dispõe do conceito de animal, assim também a Geometria só pode falar em triângulo ou quadrado, pressupondo a Aritmética (op. cit. I, 1, 20 e ss.).
[15] Já Agostinho lembra que Pitágoras nunca escreveu nada: "Nam Pythagoras(...) non tantum de se, sed nec de ulla re aliquid scripsisse perhibetur". De consensu euangelistarum,1,7,12.
[16] Sabemos muito pouco sobre Nicômaco de Gerasa (entre 55 e 166 D.C.). Autor de várias obras que se perderam. A Introdução à Aritmética foi traduzida ao latim por Apuleio, segundo Cassiodoro (PL 70, 1208 B). Também essa tradução não chegou até nós, mas somente o De institutione arithmetica de Boécio, que é uma adaptação dessa obra (Nota da ed. de José Oroz).
[17] Numerus autem est multitudo. Preferimos a forma nova multitude, pois multidão está demasiadamente associado a pessoas.
[18] A ratio, isto é, as leis e princípios racionais que neles se encerram.
[19] As partes, isto é, os divisores distintos do proprio número.
[20] Primos.
[21] Divisores.
[22] Um divisor: o um. Por vezes, quando Isidoro fala de "parte" sem mais, refere-se ao um.
[23] Não são divisíveis.
[24] Divisor.