O Operador Gradiente Vetor
André Gonçalves Antunha
(DEQ- EPUSP)
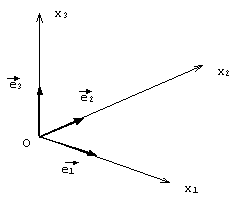
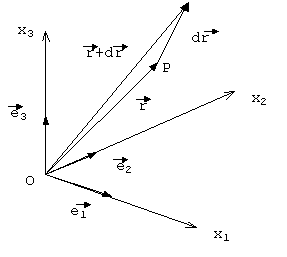
Consideremos, no espaço, um sistema de referencia de três eixos, que se cruzam em um ponto origem O, caracterizados pelos vetoresortogonais e sobre os quais são definidas respectivamente as coordenadas de posição x1 ,x2 ,x3 , como na figura:
Fig. 1 – Sistema de referência
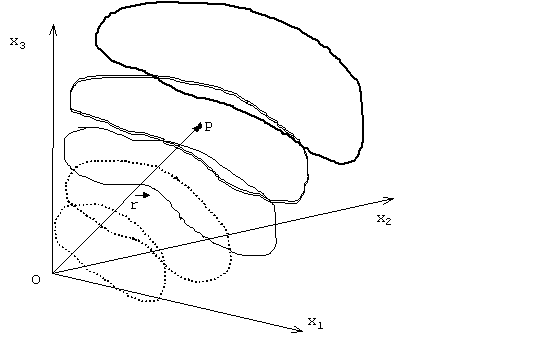
A posição de um ponto P observado é definida pelo vetor:
[1]
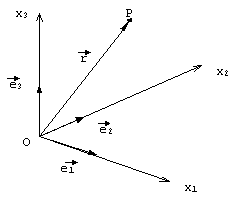
Fig. 2 Posição do Ponto P
Consideremos uma propriedade genérica j função do tempo t e da posição:
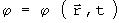
a derivada da propriedade j, em um ponto P, na posicao
, e em relação a o tempo é dada por:
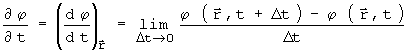
o símbolo ¶ e utilizado para explicitar que a derivada é parcial, isto é, que a derivada é realizada com variação apenas na variável considerada e mantendo-se todas as outras invariantes. No caso a derivada é apenas temporal mantendo-se constante a posição do ponto observado no espaço.
A derivada parcial da propriedade j, em um instante t, em relação aa posição é um vetor denominado gradiente de j , representado por
e definida por:
[2]
novamente o símbolo ¶ explicita que a derivada é parcial e realizada com variação apenas na posição mas mantendo-se o tempo constante. É como se fosse um deslocamento do ponto observado no espaço sem que o tempo decorresse. É portanto um deslocamento virtual. A posição do ponto observado varia mas o tempo permanece “congelado”.
Figura 3 Deslocamento do ponto observado
A idéia de tempo congelado corresponde a de um instantâneo tal como aquele que se obtém de uma fotografia. Se imaginarmos que possamos fotografar uma propriedade j genérica no espaço tridimensional e que possamos apresenta-la na forma de superfícies que reunam os pontos que apresentam o mesmo valor dessa propriedade j. A cada uma dessas superfícies corresponde um determinado valor e denominam-se iso-superfícies de j.
Consideremos, apenas para facilidade de representação que a propriedade j esteja normalizada e assuma portanto apenas valores entre 0 e 1.
Nas próximas figuras apresentaremos apenas as iso-superfícies correspondentes aos valores j = 0 ; 0,25 ; 0,5 ; 0,75 e 1 sempre com a seguinte convenção de tracejados:
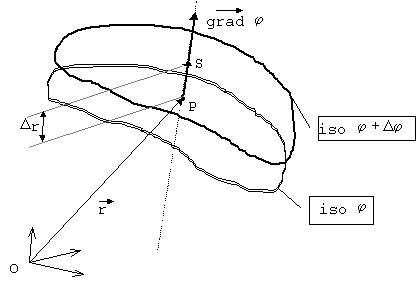
Na figura abaixo esta apresentado o campo de uma propriedade j através de suas iso-superfícies [jconstante]. Esta figura sugere uma ”fotografia“ espacial do campo em um instante no qual o tempo foi congelado, o vetor posição aponta para um ponto P cujo valor da propriedade j corresponde, segundo a convenção, a um valor j = 0,75:
De forma a se determinar o vetor gradiente de j num ponto P qualquer devemos aplicar a definição [2] que é, por sua vez, equivalente a:
[3]
Fig. 4 Iso-superfícies do campo j com tempo congelado
onde a diferencial da propriedade j equivale ao produto escalar do seu gradiente pela variação da posição observada correspondente. Para a determinação do gradiente em P efetuaremos três variações “virtuais” da posição (mantendo-se sempre o tempo congelado). Na primeira observaremos um ponto Q, distante de P de um deslocamento elementar
que se efetua sobre a mesma iso-superfície de P, como na figura abaixo.
Como P e Q estão na mesma iso-superfície a propriedade j não varia e portanto:
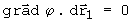
como nem
nem o gradiente são nulos eles devem ser perpendiculares entre si para o que produto escalar nulo seja satisfeito. Dessa forma o vetor gradiente que tem origem no ponto P deve estar no plano perpendicular a
:
Fig. 5 Um deslocamento vetorial sobre a isso-superfície com tempo congelado
Repetindo o procedimento para um novo deslocamento virtual elementar
ainda sobre a mesma iso-superfície mas numa direção diferente da de
chega-se também a conclusão que:
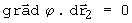
e portanto que o vetor gradiente que tem origem no ponto P deve estar também no plano perpendicular a
:
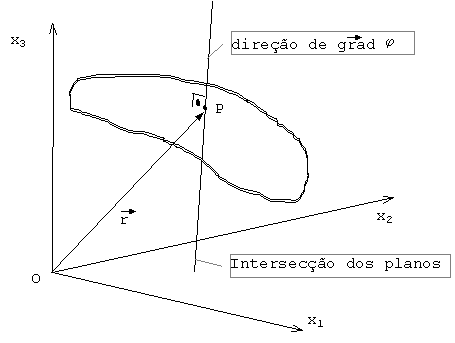
Fig. 6 Outro deslocamento vetorial e a intersecção de planos
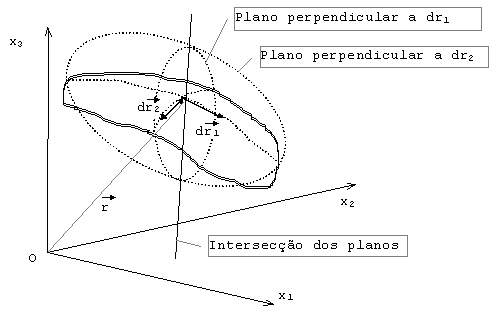
finalmente o vetor gradiente que tem origem no ponto P deve estar na interseção dos dois planos se orientando portanto segundo a perpendicular a superfície da iso-superfície de j:
Fig. 7
– Direção do gradiente é a mesma da intersecção dos planos
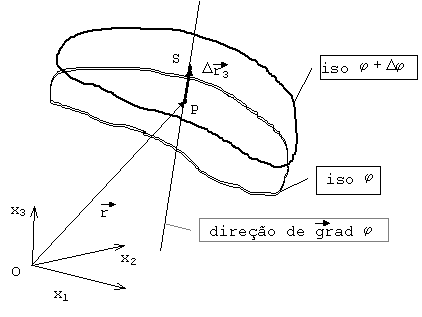
para o cálculo do módulo do vetor gradiente que tem origem no ponto P consideremos mais um deslocamento virtual
agora segundo a perpendicular aa iso-superfície de j, com origem nela e terminando num ponto S na iso-superfície j + Dj:
Fig. 8 Um deslocamento vetorial entre duas isso-superfícies na direção do gradiente
aplicando a definição [2]:
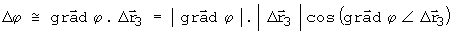
mas como
esta na direção de
eles são paralelos e o angulo entre eles é nulo e o seu coseno unitário:

assim o módulo de
é:
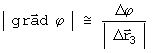
Resumindo: o vetor gradiente de uma função de estado genérica j, que tem origem num ponto P qualquer, aponta sempre na direção perpendicular aa iso-superfície de j que passa pelo ponto P considerado. Ele indica a direção de maior variação de j com a posição. Ele tem modulo igual a divisão entre a diferença do valor da função j de duas iso-superfícies próximas pela distancia entre elas, para um limite de duas iso-superfícies muito próximas [a distancia considerada sobre a perpendicular às iso-superfícies e que passa pelo ponto P deve “tender a zero”]. O seu sentido é arbitrado de forma a apontar sempre para valores de j crescentes:
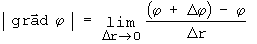
Fig. 9 Módulo do gradiente
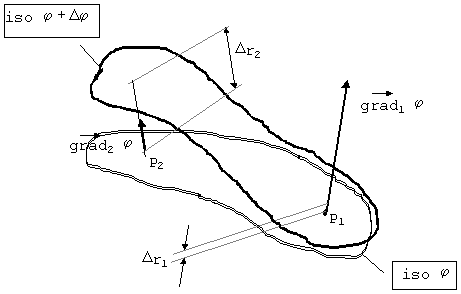
Dessa forma fica evidente que quanto mais próximas forem duas iso-superfícies o gradiente será sempre maior nos pontos onde a distância entre elas for menor.
Fig. 10 Variação do gradiente no espaço
Admitindo que o sistema de referencia é cartesiano, com coordenadas x, y e z, o estado estático da função j genérica é definido por:
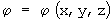
a sua diferencial é portanto por definição:
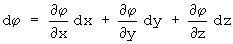
Já o vetor posição que escreve-se:
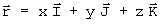
tem sua derivada:
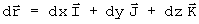
por sua vez o gradiente em coordenadas cartesianas:
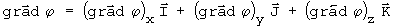
aplicando a definição de gradiente [2]:
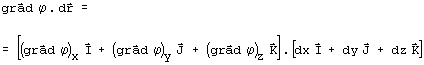
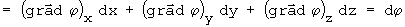
então:
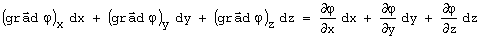
como dx, dy e dz são linearmente independentes:
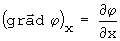
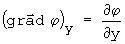
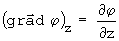
introduzindo no gradiente:
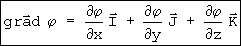
que é equivalente aa aplicação direta do “operador gradiente em coordenadas cartesianas” comumente apresentado nos livros de matemática e representado por:
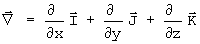
Exercício 1) Como o vetor posição em coordenadas cilíndricas ( r, f, z) escreve-se como:
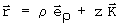
e sua derivada:
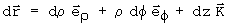
demonstrar que o gradiente em coordenadas cilíndricas é:
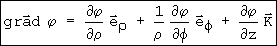
Exercício 2) O vetor posição em coordenadas esféricas ( r, q, f) escreve-se como:

e sua derivada:
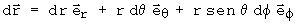
demonstrar que o gradiente em coordenadas cilíndricas é:
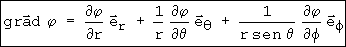
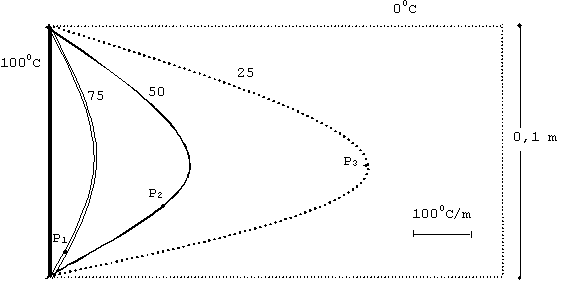
Exercício 3) Para um campo de temperaturas bidimensional em uma placa plana de 10 x 18 cm descrito na figura abaixo esboçar (na escala apresentada) os vetores do gradiente de temperatura para os pontos assinalados:
Fig. 11 Um campo de temperatura
Bibliografia:
Sales Luis, A C. Introdução à Termofísica, apostila, UNICAMP, 1977