Cálculo da Pressão de Vapor
de Componentes Puros Utilizando
Equações de Estado Cúbicas
Débora J. Araújo; Karla A. de Freitas;
Diogo C. Crispim, Moilton R. Franco Jr.
Fac. de Eng. Química –Univ. Federal de Uberlândia
moilton@ufu.br -Santa Mônica - 38408-100
Uberlândia – MG
Abstract
In this work is proposed a technique applying cubic equations of state (EOS) to the calculations of vapor pressures of pure compounds. The procedure employed considers that in the small temperature range, vapor pressure is approximately equal the zero-pressure liquid fugacity. The cohesion function, a(Tr), used in this work was proposed by Stryjek and Vera (1986) and the cubic equations of state were van der Waals (vdW), Redlich Kwong (RK) and Peng Robinson (PR), (Walas, 1985). The method proposed showed to be an efficient technique for the prediction of vapor pressure.
Keywords: Equations of state; vapor pressure, predictive method
Resumo
Neste trabalho é proposta uma técnica aplicando equações de estado cúbicas no cálculo da pressão de vapor de componentes puros. O procedimento adotado considera que em pequenas faixas de temperatura, a pressão de vapor é aproximadamente igual à fugacidade do líquido na pressão zero. A função de coesão, a(Tr), utilizada neste trabalho foi a de Stryjek e Vera (1986) e as equações de estado cúbicas foram as de van der Waals (vdW), Redlich Kwong (RK) e Peng Robinson (PR), (Walas, 1985). O método proposto mostrou ser uma técnica eficiente para a predição da pressão de vapor.
Palavras chave: Equações de estado, pressão de vapor, predição.
INTRODUÇÃO
Em 1997, Segura e Wisniak propuseram um algoritmo eficiente para resolver problemas de pressão de vapor de componentes puros utilizando equações de estado cúbicas (Reid et al., 1987). Eles mostraram que a fugacidade do líquido na pressão zero (fL,0) é uma aproximação assintótica da pressão de vapor predita pelas equações de estado em baixas temperaturas reduzidas (Tr £ 0,5).
Neste trabalho, é proposto um procedimento direto para a estimativa da função a(Tr) em baixas temperaturas. O procedimento é baseado no estado de referência de pressão zero e é aplicado no ponto triplo (onde ele torna-se praticamente exato) para o ponto normal de ebulição. Os valores de a(Tr) podem ser obtidos usando correlações empíricas bem estabelecidas, cuja extrapolação para a faixa crítica mostra uma concordância com os dados semi-experimentais da pressão de vapor. Desenvolvimentos e ilustrações são verificados através do emprego de equações de estado cúbicas.
TEORIA
Equações de estado cúbicas podem ser generalizadas de acordo com a Equação 1.
(1)
onde P é a pressão, T é a temperatura, V é o volume específico, a é o parâmetro de coesão que ocorre devido às forças atrativas, b é o co-volume que considera o empacotamento de moléculas, u e w são valores (ou equações) encontrados na Tabela 1. Existem várias aproximações que podem ser usadas para determinar os parâmetros a e b, uma delas é escolher a e b para que as condições do ponto crítico sejam satisfeitas:
(2a)
(2b)
Aplicando a Equação 2(a,b) em 1, obtém-se os valores de a e b, para diferentes equações de estado cúbicas, que se encontram especificadas na Tabela 1.
O termo de coexistência (ou coesão) da equação cúbica é função da temperatura de acordo com a Equação 3.
(3)
Neste trabalho os parâmetros b, c e d (Tabelas 1 e 2) são considerados iguais aos parâmetros críticos em toda a faixa PVT, assim,
(4)
A expressão empírica mais usada, que mostra a dependência do parâmetro de coexistência com a temperatura, foi proposta por Soave (1972) e é dada pela Equação 5:
(5)
Na Equação 5, m(w) é uma função generalizada do fator acêntrico.
Tabela 1: Constantes e expressões pertencentes ás equações de estado cúbicas.
Equação
u
w
B
A
vdW
0
0
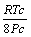
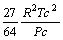
RK
1
0


PR
2
-1
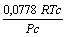
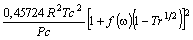
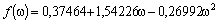
Outros modelos existentes para a função a(Tr), podem ser conferidos na Tabela 2.
Tabela 2: Correlações para a dependência de a com a temperatura.
Mathias e Copeman (1983)

Soave (1984)

Stryjek e Vera (1986)
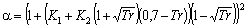
Androulakis et al., (1989)
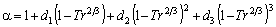
Melhem et al., (1989)
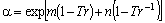
ci, Ki, di, m, n são constantes específicas que dependem de propriedades termodinâmicas do componente.
O valor das fugacidades (f) pode ser obtido da Equação 6, usando a relação clássica (Walas, 1985):
(6)
O volume de líquido na pressão zero (V0) pode ser calculado a partir da Equação 7:
(7)
em que u é dado pela Equação 8:
(8)
O parâmetro x é dado pela Equação 9:
(9)
O volume considerado e a pressão de vapor limite da Equação 6, aplicados a Equação 1, determina-se a fugacidade do líquido na pressão zero (fL,0) dada por:
(10)
em que os parâmetros l0 e q0 são calculados da seguinte forma:
(11)
(12)
(13)
Observando-se as Equações de 8 a 13 vê-se que a fugacidade depende somente da temperatura e pode ser calculada seguindo a metodologia que se segue:
(a) Dados as propriedades críticas Tc, Pc e a temperatura T, calcula-se os valores ac, bc, cc e dc.
(b) Conhecendo-se o valor de a(Tr), calcula-se o parâmetro de coexistência pela Equação 3 e os demais parâmetros pela Equação 4;
(c) A partir da Equação 8, calcula-se o parâmetro u;
(d) A fugacidade do líquido na pressão zero é calculada utilizando as Equações 10 – 13.
Como observado por Segura e Wisniak (1997), a fugacidade do líquido na pressão zero pode ser usada para aproximar a pressão de vapor a temperaturas reduzidas baixas,
(14)
com erros máximos de 1% para uma faixa de Tr £ 0,5, para uma equação de estado cúbica padrão. Esta faixa, no entanto, pode ser ampliada usando a seguinte aproximação mais rigorosa da condição de equilíbrio, (Walas, 1985):
(15)
Considerando que a fugacidade na fase líquida é uma função fraca da pressão e que em faixas de pressões moderadas a fugacidade da fase vapor pode ser aproximada pelo equação de virial truncada no segundo termo, tem-se que uma expressão para fL,0 pode ser dada por:
(16)
onde B* é o segundo coeficiente do virial, como o calculado a partir de uma equação de estado cúbica,
(17)
Pela Equação 16, nota-se não são necessárias muitas informações para o cálculo da fL,0 já que a única variável desconhecida é a pressão de vapor.
A Equação 16 pode ser reescrita da seguinte forma:
(18)
Segundo Wisniak et al., 1998, a faixa onde a fugacidade do líquido na pressão zero se aproxima da pressão de vapor com erro máximo de 1% para diferentes valores do fator acêntrico (uma faixa 0 < w < 0,8). A Equação 16 permite aproximações da pressão de vapor em faixa mais ampla de temperaturas. Especificamente, as pressões de vapor são melhores aproximadas para Tr = 0,7. Esta equação pode ser empregada de duas formas, a saber:
(a) Uma que permite uma excelente aproximação da pressão de vapor, quando as equações de estado cúbicas e a função a(Tr) são conhecidas;
(b) Para estimar o valor de a(Tr) que interpola dados de pressão de vapor na faixa de temperatura, onde a aproximação com a fugacidade do líquido na pressão zero é aplicável. Neste caso, uma vez que os parâmetros críticos podem ser determinados e as condições de saturação (Psat, T) são conhecidas, o problema reduz a encontrar o valo r de x. A função a(Tr) pode ser obtida por:
(19)
Embora os cálculos apresentados acima pareçam ser complexos, pode-se observar que nenhum cálculo volumétrico é preciso para a Equação 1. De fato o procedimento iterativo é mais simples e eficiente do que a solução rigorosa do problema da pressão de bolha.
A Equação 16 combinada com a Equação 17 pode ser escrita na forma da seguinte função objetiva:
(20)
O método de Newton-Raphson é altamente recomendado para essa proposição, usando o seguinte valor inicial:
(21)
Com o procedimento indicado, três ou quatro iterações são usualmente necessárias para a convergência.
APLICAÇÕES DO MÉTODO PROPOSTO
Para testar a validade da aproximação proposta serão estimados os parâmetros da função a(Tr) proposta por Stryjek e Vera que depende de dois parâmetros (K1 e K2). Neste trabalho usou-se a seguinte metodologia:
(a) A função a(Tr) pode ser obtida usando dois pontos da pressão de vapor. Um ponto que corresponde ao limite inferior de temperatura em que se aplica a correlação de Antoine e o outro é o ponto normal de saturação;
(b) Usando os valores de a(Tr) obtidos, como descrito no item (a), os dois parâmetros da correlação de Stryjek e Vera puderam ser estimados para cada componente;
(c) Obtida a correlação a(Tr), pode-se predizer a pressão de vapor na faixa de validade da equação de Antoine.
Neste trabalho, os compostos utilizados no cálculo da pressão de vapor, a partir das equações de estado cúbicas de van der Waals, Redlich-Kwong e Peng-Robinson foram: n-pentano, acetona, benzeno, ciclohexano e tolueno, cujas propriedades críticas foram obtidas no Reid et al. (1987).
A pressão de saturação utilizada como base para as comparações foi calculada através da equação de Antoine, cujas constantes foram obtidas em Himmelblau (1984).
RESULTADOS E DISCUSSÕES
A Tabela 3 apresenta os resultados obtidos pelo método proposto, para a predição da pressão de saturação usando aproximação com a fugacidade do líquido na pressão zero (0,5 < Tr < 0,99).
Pode–se observar que para os componentes: n-pentano, acetona e tolueno, a equação de estado cúbica de Peng-Robinson foi a que apresentou um menor erro entre a pressão de saturação calculada por Antoine e a pressão obtida pelo método proposto, seguida da equação de Redlich-Kwong.
Tabela 3: Predição de Psat usando aproximação com a fugacidade do líquido na pressão zero (0,5 < Tr < 0,99)
Componentes
T(K)
Psat (bar)
Antoine
van der Waals
ER(%)
Redlich-Kwong
ER(%)
Peng-Robinson
ER(%)
n-pentano
300
0,71384
0,68743
3,69
0,69431
2,73
0,69595
2,50
305
0,85435
0,81171
4,99
0,86010
0,67
0,85545
0,12
308
0,94855
0,90357
4,74
0,97232
2,50
0,96250
1,47
310
1,01573
0,96925
4,57
1,05269
3,63
1,03874
2,26
312
1,08658
1,03865
4,41
1,13764
4,69
1,11898
2,98
Média (Erro)
4,48
2,85
1,87
Acetona
330
1,00674
0,97117
3,53
0,98497
2,16
0,98656
2,00
335
1,18993
1,15206
3,18
1,19938
0,79
1,19567
0,48
338
1,31198
1,27298
2,97
1,34316
2,37
1,33500
1,75
340
1,39873
1,35908
2,83
1,44568
3,35
1,43385
2,51
350
1,90308
1,86150
2,18
2,04264
7,33
2,00237
5,21
Média (Erro)
3,33
3,20
2,39
Benzeno
345
0,76071
0,73090
3,92
0,72286
4,98
0,70634
7,15
350
0,89286
0,85959
3,72
0,88281
1,12
0,85559
4,17
355
1,04232
1,00583
3,50
1,06748
2,41
1,02640
1,52
353
0,98035
0,94513
3,59
0,95292
2,79
0,95540
2,54
Média (Erro)
3,50
2,83
3,85
Ciclohexano
370
1,56527
1,51202
3,40
1,49199
4,68
1,61374
3,09
375
1,78869
1,73162
3,19
1,7395
2,74
1,86349
4,18
373
1,69657
1,64103
3,27
1,63531
3,61
1,76084
3,78
Média (Erro)
3,28
3,67
3,68
Tolueno
380
0,88637
0,84832
4,29
0,84083
5,13
0,83820
5,43
385
1,02283
0,98250
3,94
0,99868
2,36
0,98997
3,21
390
1,17529
1,13307
3,59
1,17700
0,14
1,16000
1,30
395
1,34498
1,30134
3,24
1,37694
2,37
1,34906
0,30
410
1,97047
1,92553
2,28
2,11655
7,41
2,03583
3,31
393
1,27496
1,23183
3,38
1,29430
1,51
1,271113
0,30
Média (Erro)
3,45
3,15
2,31
Para todas as equações de estado cúbicas utilizadas encontraram-se erros inferiores a 5% no cálculo da pressão de saturação, sendo que para determinadas temperaturas, o erro foi inferior a 1%. O erro relativo foi calculado através da expressão:
(22)
Os resultados publicados estão dentro da faixa de temperatura de 0,5 < Tr < 0,99, pois nesta faixa, o método proposto parece ser mais preciso no cálculo da pressão de saturação.
CONCLUSÕES
As conclusões obtidas neste trabalho foram:
· No cálculo da pressão de saturação, a equação de Peng-Robinson apresentou os menores erros relativos;
· O método proposto para o cálculo da pressão de saturação é simples, visto que requer apenas dois valores de pressão de vapor, sendo que um deles é o ponto normal de ebulição;
· A equação proposta por Stryjek e Vera (1986), para o cálculo de a(Tr) mostrou-se acurada para uma adequada representação da pressão de vapor de componentes puros.
SIMBOLOGIA
a Parâmetro de coesão;
B* Segundo coeficiente do virial;
b Covolume;
c,d Parâmetro adicional;
A, B, C, D Parâmetros admensionais;
f Fugacidade;
K1, K2 Parâmetros da correlação de Stryjek e Vera.;
m Parâmetro da função de Soave na Eq.5;
n Parâmetro da função a(Tr);
P Pressão;
R Constante universal dos gases;
T Temperatura;
Letras gregas
a(Tr) Parâmetro de coexistência , dependente da temperatura;
q Parâmetro definido na Eq. 12;
l Parâmetro definido na Eq. 13;
x Parâmetro definido na Eq. 9;
t Parâmetro definido na Eq. 11;
w Fator acêntrico;
Á Função objetiva definida na Eq.20;
Subscritos
c No ponto crítico;
r Propriedade reduzida;
Sobrescritos
0 Propriedade na pressão zero;
L Fase líquida;
V Fase vapor;
sat Estado de equilíbrio líquido vapor;
-1 Função inversa.
Abreviações
EOS* Equação de Estado Cúbica;
PR Equação de Peng-Robinson;
PVT Pressão-Volume-Temperatura;
RK Redlich-Kwong;
vdW van der Waals.
REFERÊNCIAS BIBLIOGRÁFICAS
Androulakis, J., Kalospiros, N.e Tassios, D., (1989), Thermophysical properties of pure polar and nonpolar compounds with modified vdW-711 equation of state. Fluid Phase Equilibria 45, 135-163.
Himmelblau, D. M., (1984), Engenharia Química Princípios e Cálculos, quarta edição, Prentice/Hall do Brasil.
Mathias, P. and Copeman, T., (1983), Extension of the Peng-Robinson equation of state to polar fluids and fluids mixtures. Fluid Phase Equilibria 13, 91-108.
Melhem, G., Saini, R. e Goodwin, B., (1989), A modified Peng-Robinson equation of state. Fluid Phase Equilibria 47, 189-37.
Reid, R. C., Prausnitz, J. M., Poling B. E., (1987), The Properties of Gases and Liquids, McGraw-Hill, New York.
Segura, H. e Wisniak, J., (1997), Calculation of pure saturation properties using cubic equations of state. Computers and Chemical Engineering, 21(12), 1339-1347.
Soave G., (1972), Improvement of the van der Waals equation of state. Chem. Engng Sci. 31, 203-207.
Soave G., (1984), Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Engng Sci. 27, 1197-1203.
Stryjek, R. e Vera, J. H.,(1986), PRSV: An improved Peng-Robinson equation of state for pure compounds and mixtures. Can. J. Chem. Engng, 64, 323-333.
Walas, S., M., (1985), Phase Equilibria in Chemical Engineering, Butterworth Publis.
Wisniak, J., Apelblat, A., Segura H., (1998), Aplication of Cubic Equations of State to fit vapor pressures of Pure Components, Chemical Engineering Science, Vol.53, No4, 743-751.